Uniforms
Apparently
vec4rgba()As a Creative Front-End Developer I wanted to learn more about WebGL. WebGL is generally used for 2D and 3D animation on the web because it enables GPU rendering, which makes it fast. This one-pager will contain all the information that I learn from the https://thebookofshaders.com/
Hover on a block with a canvas to reveal the Fragment Shader code that's used in the example.
Apparently
vec4rgba()u_timeu_resolutiongl_FragColor = vec4(abs(sin(u_time)),abs(u_mouse.x*0.001),abs(u_mouse.y*0.001) ,1.0);This is where I got a headache. The x and y coordinates of the fragment get divided by the resolution which results in the fragment being diagonal which then are multiplied by the a function of passed time in second
vec2 st = gl_FragCoord.xy/u_resolution;
gl_FragColor = vec4(abs(cos(u_time * st.x)),abs(sin(u_time * st.y)),abs(sin(u_time * st.y * st.x)),1.0);We visualize the normalized value of the x coordinate (st.x) in two ways: one with brightness (observe the nice gradient from black to white) and the other by plotting a green line on top (in that case the x value is assigned directly to y). The line visualizes the gradient. Updating float y changes the line and gradient.
The fragment shader in lesson 5
float y = smoothstep(0.2,0.5,st.x) - smoothstep(0.5,0.8,st.x);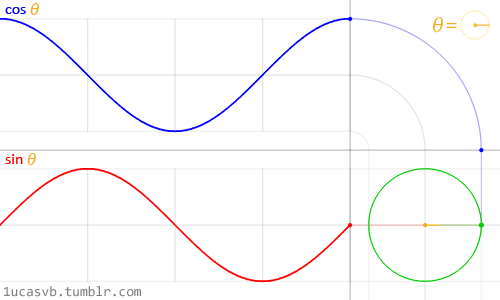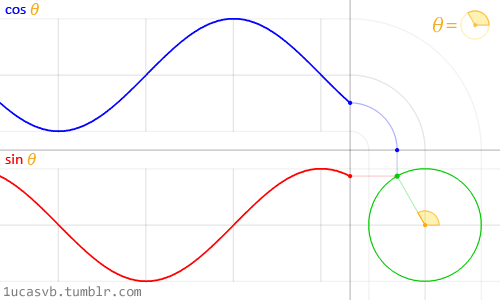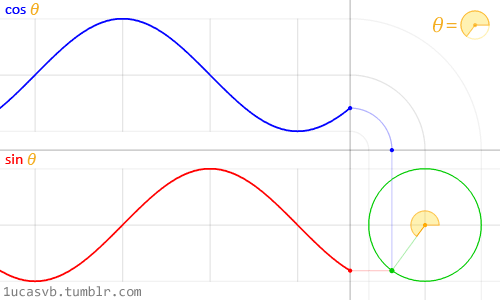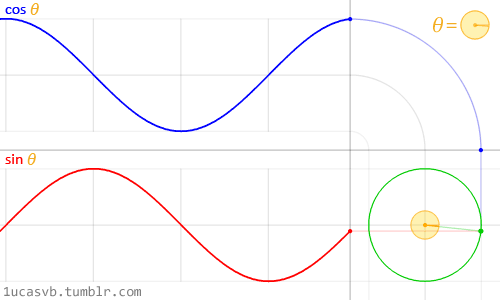
"The values of .x, .y and .z can also be called .r, .g and .b, and .s, .t and .p. (.s, .t and .p are usually used for spatial coordinates of a texture, which we'll see in a later chapter.) You can also access the data in a vector by using the index position, [0], [1] and [2]." - https://thebookofshaders.com/06/
vec4 vector;
vector[0] = vector.r = vector.x = vector.s;
vector[1] = vector.g = vector.y = vector.t;
vector[2] = vector.b = vector.z = vector.p;
vector[3] = vector.a = vector.w = vector.q;"In GLSL there is a very useful function, mix(), that lets you mix two values in percentages. Can you guess what the percentage range is? Yes, values between 0.0 and 1.0! Which is perfect for you, after those long hours practicing your karate moves with the fence - it is time to use them!" - https://thebookofshaders.com/edit.php#06/easing.frag
https://thebookofshaders.com/06/
I feel like this plot displays this lesson clearly. Colors are plotted on the canvas the same way as lines are. The colors all mix together.
pct.r = smoothstep(0.2,0.0, st.y);
pct.g = smoothstep(st.x*0.1,st.x*0.0,st.y*0.1);
pct.b = pow(st.y,0.5);To animate the circular rainbow I added the cosinus function of passed time which results in an ease that I can speed up or slow down by multiplying it.
color = hsb2rgb(vec3((angle/TWO_PI)+cos(u_time) * 0.5,radius,1.0));
In WebGL you can give the parameters of a function a type much like in TypeScript.
int newFunction(in vec4 aVec4, // read-only
out vec3 aVec3, // write-only
inout int aInt); // read-writeUsing Math to draw things is hard. This function contains the Math to draw a square. It makes a "step" from the bottom left to top left and bottom right. If we multiply the positions of bottom left with top right it returns the used space of the function.
// bottom-left
vec2 bl = step(vec2(0.1),st);
float pct = bl.x * bl.y;
// top-right
vec2 tr = step(vec2(0.1),1.0-st);
pct *= tr.x * tr.y;This circle is pretty much a radial gradient but I removed the gradient part to just end up with a circle. This was pretty much done with magic numbers. You can look at this circle and radial gradients as if you were hovering over a mountain and looking straight down onto it.
float pct = 0.0;
vec2 tC = vec2(15.5)-st*31.0;
pct = sqrt(tC.x*tC.x+tC.y*tC.y-15.5);
vec3 color = vec3(pct);
gl_FragColor = vec4( color, 1.0 );In Math creating a circle revolves around setting the radius from middle to side and multiplying this to PI*2. A lot of everyday functions like creating a circle are premade by people and shared by websites like Shadertoy.
This gradient is created by constantly updating the distance field of the gradient:
d = length( max(abs(st * abs(cos(u_time*0.5)))-.0,0.) );gl_FragColor = vec4(vec3( smoothstep(.1,.4,d)* smoothstep(.6,.55,d)) ,1.0);vec2 pos = vec2(0.5)-st;
float r = length(pos)*2.0;
float a = atan(pos.y,pos.x);
"In the chapter about color we map the cartesian coordinates to polar coordinates by calculating the radius and angles of each pixel with the following formula:" - https://thebookofshaders.com/07/
The displayed function pretty much takes the radius and bends it from a certain degree to another with the mathematical atan function
So... This shape is a result of using:
f = smoothstep(-.5,1., cos(a*10.))*0.2+0.5;float q = abs(cos(a*12.)*sin(a*3.))*.8+.2;color = 1.0 * color+pct * vec3(abs(sin(u_time*0.5)),abs(cos(u_time*0.5)),abs(tan(u_time*0.5)));float a = atan(pos.y,pos.x) +PI*(u_time*0.25);
This is where I wrote my first ever (working) WebGL function! It works by returning a shape.
vec3 makeShape(vec2 st, int N){
float d = 0.0;
// Remap the space to -1. to 1.
st = st *2.-1.;
// Angle and radius from the current pixel
float a = atan(st.x,st.y)+PI;
float r = TWO_PI/float(N);
d = cos(floor(.5+a/r)*r-a)*length(st);
return vec3(1.0-smoothstep(.4,.41,d));
}color = makeShape(st, 3);I can say that I have learned that fragment shaders are pretty much textures calculated by Math. The Math involved really feels like the Math I learned in Highschool, you are pretty much constantly calculating points and connections in a certain area.
For now this is where my journey through fragment shader land reaches to a halt. The Book of Shaders contains a lot of information about fragment shaders and apparently I made it through the rough part. After this little project I will be learning more from the Book of Shaders which I will document on my CodePen account: https://codepen.io/meesrutten